HW3 詳解

Question 1

問題1

page 226, chapter 3.2 Example 9

Give a big-$O$ estimate for $f(n) = 3n \log(n!) + (n^2 + 3) \log n$, where n is a positive integer.

問題1

page 214, chapter 3.1 Exercises 24

Give a big-$O$ estimate for $f(n) = 3n \log(n!) + (n^2 + 3) \log n$, where n is a positive integer.

First, the product $3n \log(n!)$ will be estimated. From Example 6 we know that $\log(n!)$ is $O(n \log n)$. Using this estimate and the fact that $3n$ is $O(n)$, Theorem 3 gives the estimate that $3n \log(n!)$ is $O(n^2 \log n)$. Next, the product $(n^2 + 3) \log n$ will be estimated. Because $(n^2 + 3) < 2n^2$ when $n > 2$, it follows that $n^2 + 3$ is $O(n^2)$. Thus, from Theorem 3 it follows that $(n^2 + 3) \log n$ is $O(n^2 \log n)$. Using Theorem 2 to combine the two big-$O$ estimates for the products shows that $f(n) = 3n \log(n!) + (n^2 + 3) \log n$ is $O(n^2 \log n)$.

Question 2

問題2

page 228, Section 3.2 Exercise 2

Determine whether each of these functions is $O(x^2)$.

$f(x) = 17x + 11$
$f(x) = x^2 + 1000$
$f(x) = x log x$
$f(x) = x^4/2$
$f(x) = 2^x$
$f(x) = ⌊x⌋ ⋅ ⌈x⌉$

問題2

page 228, Section 3.2 Exercise 2

Determine whether each of these functions is $O(x^2)$.

$f(x) = 17x + 11$
$f(x) = x^2 + 1000$
$f(x) = x log x$
$f(x) = x^4/2$
$f(x) = 2^x$
$f(x) = ⌊x⌋ ⋅ ⌈x⌉$

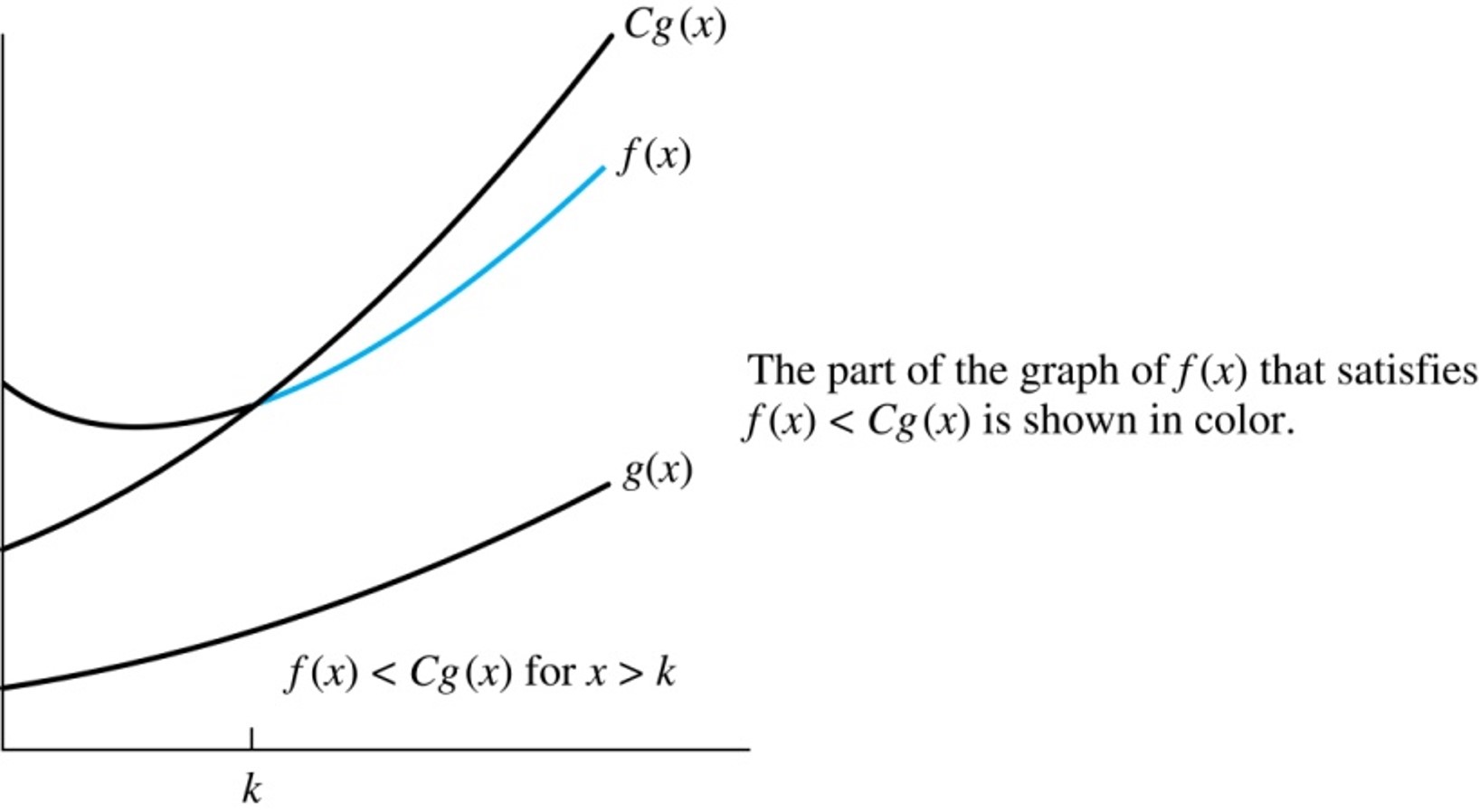
Big-O notation

Let f and g be functions from the set of integers or the set of real numbers to the set of real numbers.
We say that $f(x)$ is $O(g(x))$ if there are constants C and k such that $|f(x)| \leq C|g(x)|$ whenever $x > k$.

Yes, since $17x+11\leq17x+x=18x\leq18x^2$ for all $x>11$, $C = 18, k = 11$.
Yes, since $x^2+1000\leq x^2+x^2=2x^2$ for all $x>\sqrt{1000}$, $C = 2, k = \sqrt{1000}$.
Yes, since $xlogx\leq x\cdot x=x^2$ for all $x$, $C = 1, k = 0$.
No, If there were a constant $C$ such that $x^4/2\leq Cx^2 $ for sufficiently large $x$, then we would have $C\geq x^2/2$.
No, If $2^x$ were $O(x^2)$, then the fraction $2^x/x^2$ would have to be bounded above by some constant $C$.
Yes, since $\lfloor x \rfloor \lceil x \rceil\leq x(x+1)\leq x\cdot2x = 2x^2$ for all $x>1$, C = 2, k = 1.

Question 3

問題3

page 241, Section 3.3 Exercise 2

Give a big-O estimate for the number additions used in this segment of an algorithm.

              
                t := 0
                for i := 1 to n
                for j := 1 to n
                t := t + i + j

問題3

page 241, Section 3.3 Exercise 2

Give a big-O estimate for the number additions used in this segment of an algorithm.

              
                t := 0
                for i := 1 to n
                for j := 1 to n
                t := t + i + j

The statement $t := t + i + j$ is executed $n^2$ times, so the number of operations is $O(n^2)$.