HW6 詳解
問題1
page 418, chapter 6.1 Exercise 36
How many functions are there from the set {1, 2, ... , n},
where n is a positive integer, to the set {0, 1}?
where n is a positive integer, to the set {0, 1}?
問題1
page 418, chapter 6.1 Exercise 36
How many functions are there from the set {1, 2, ... , n},
where n is a positive integer, to the set {0, 1}?
where n is a positive integer, to the set {0, 1}?
There are $2^n$ such functions, since there is a choice of 2
function values for each element of the domain.
問題2
page 444, chapter 6.4 Exercise 10
Use the binomial theorem to expand $(3x - y^2)^4$ into a sum
of terms of the form $cx^ay^b$, where c is a real number and
a and b are nonnegative integers.
問題2
page 444, chapter 6.4 Exercise 10
Use the binomial theorem to expand $(3x - y^2)^4$ into a sum
of terms of the form $cx^ay^b$, where c is a real number and
a and b are nonnegative integers.
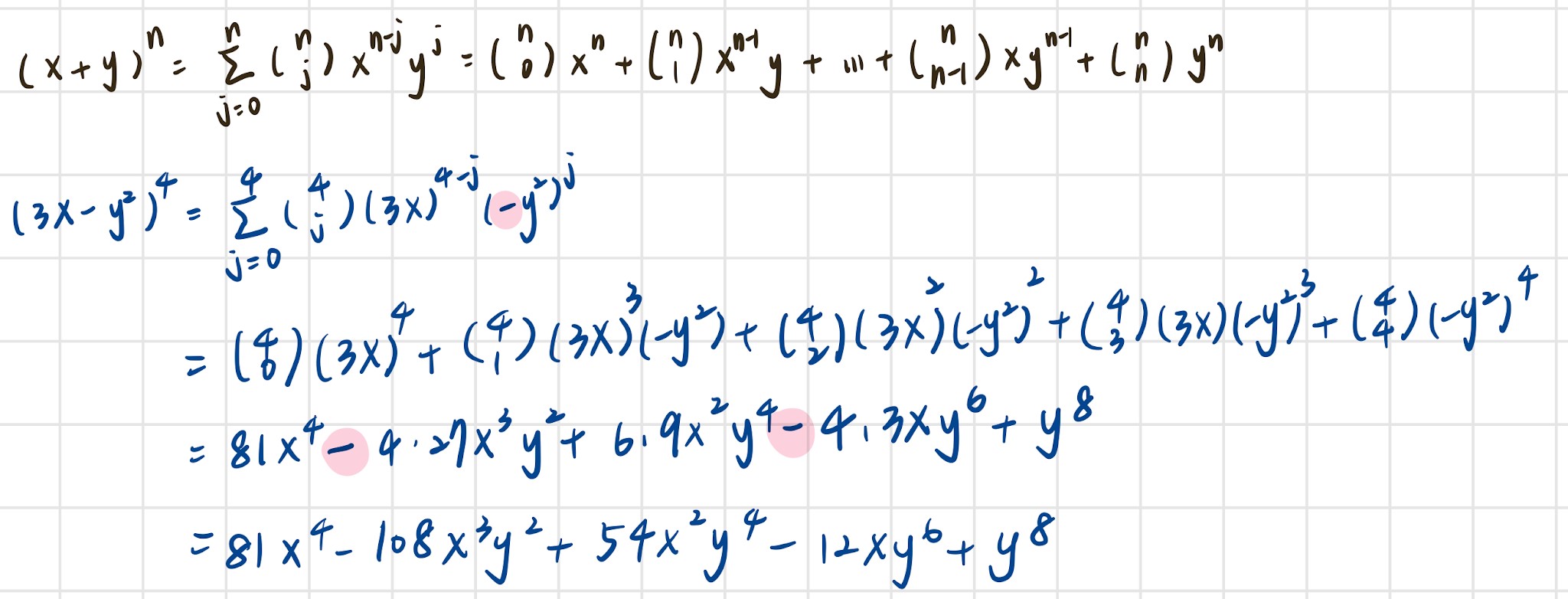
問題3
page 455, chapter 6.5 Exercise 14
How many solutions are there to the equation
\begin{eqnarray*}
x_1 + x_2 + x_3 + x_4 = 17,
\end{eqnarray*}
where $x_1$, $x_2$, $x_3$, and $x_4$ are nonnegative integers?
問題3
page 455, chapter 6.5 Exercise 14
How many solutions are there to the equation
\begin{eqnarray*}
x_1 + x_2 + x_3 + x_4 = 17,
\end{eqnarray*}
where $x_1$, $x_2$, $x_3$, and $x_4$ are nonnegative integers?
\begin{eqnarray*}
C(\underline{4} + \underline{17} - 1, \underline{17}) = C(20, \underline{17}) = \underline{1140}
\end{eqnarray*}
問題4
page 455, chapter 6.5 Exercise 16
How many solutions are there to the equation
\begin{eqnarray*}
x_1 + x_2 + x_3 + x_4 + x_5+ x_6= 29,
\end{eqnarray*}
where $x_i$, $i$ = 1, 2, 3, 4, 5, 6, is a nonnegative integer such that
- $x_i > 1$ for $i$ = 1, 2, 3, 4, 5, 6 ?
- $x_1 \ge 1$, $x_2 \ge 2$, $x_3 \ge 3$, $x_4 \ge 4$, $x_5 > 5$, and $x_6 \ge 6$ ?
- $x_1 \le 5$ ?
- $x_1 < 8$ and $x_2 > 8$ ?
How many solutions are there to the equation
\begin{eqnarray*}
x_1 + x_2 + x_3 + x_4 + x_5+ x_6= 29,
\end{eqnarray*}
where $x_i$, $i$ = 1, 2, 3, 4, 5, 6, is a nonnegative integer such that
- $x_i > 1$ for $i$ = 1, 2, 3, 4, 5, 6 ?
- $x_1 \ge 1$, $x_2 \ge 2$, $x_3 \ge 3$, $x_4 \ge 4$, $x_5 > 5$, and $x_6 \ge 6$ ?
- $x_1 \le 5$ ?
- $x_1 < 8$ and $x_2 > 8$ ?
- We require each $x_i \ge 2$ . This uses up 12 of the 29 total required, so the problem is the same as finding the number of solutions to $x'_1 + x'_2 + x'_3 + x'_4 + x'_5 + x'_6 = 17$ with each $x'_i$ a nonnegative integer. The number of solutions is therefore $C(6 + 17 - 1, 17) = C(22, 17) = 26334$.
- The restrictions use up 22 of the total, leaving a free total of 7. Therefore the answer is $C(6 + 7 - 1, 7) = C(12, 7) = 792$.
- The number of solutions without restriction is $C(6 + 29 - 1, 29) = C(34, 29) = 278256$. The number of solution violating the restriction by having $x_1 \ge 6$ is $C(6 + 23 - 1, 23) = C(28, 23) = 98280$. Therefore the answer is $278256 - 98280 = 179976$.
- The number of solutions with $x_2 \ge 9$ (as required) but without the restriction on $x_1$ is $C(6 + 20 - 1, 20) = C(25, 20) = 53130$. The number of solution violating the additional restriction by having $x_1 \ge 8$ is$C(6 + 12 - 1, 12) = C(17, 12) = 6188$. Therefore the answer is $53130 - 6188 = 46942$.
問題5
page 455, chapter 6.5 Exercise 20
How many solutions are there to the inequality
\begin{eqnarray*}
x_1 + x_2 + x_3 \le 11,
\end{eqnarray*}
where $x_1$, $x_2$, and $x_3$ are nonnegative integers?
[Hint: Introduce an auxiliary variable $x_4$ such that $x_1 + x_2 + x_3 + x_4 = 11$.]
問題5
page 455, chapter 6.5 Exercise 20
How many solutions are there to the inequality
\begin{eqnarray*}
x_1 + x_2 + x_3 \le 11,
\end{eqnarray*}
where $x_1$, $x_2$, and $x_3$ are nonnegative integers?
[Hint: Introduce an auxiliary variable $x_4$ such that $x_1 + x_2 + x_3 + x_4 = 11$.]
\begin{eqnarray*}
C(\underline{4} + \underline{11} - 1, \underline{11}) = C(14, \underline{11}) = \underline{364}
\end{eqnarray*}
問題6
page 457, chapter 6.5 Exercise 64
How many different terms are there in the expansion of
\begin{eqnarray*}
(x_1 + x_2 + ... + x_m)^n
\end{eqnarray*}
after all terms with identical sets of exponents are added?
問題6
page 457, chapter 6.5 Exercise 64
How many different terms are there in the expansion of
\begin{eqnarray*}
(x_1 + x_2 + ... + x_m)^n
\end{eqnarray*}
after all terms with identical sets of exponents are added?
Each term must be of the form $Cx_1^{n_1} x_2^{n_2} ... x_m^{n_m}$,
where the $n_i$'s are nonnegative integers whose sum is n.
The number of ways to specify a term, then,
is the number of nonnegative integer solutions to $n_1 +n_2 + ... +n_m = n$,
which by Theorem 2 is $C(m + n - 1, n)$.
Note that the coefficients C for these terms can be computed using Theorem 3—see Exercise 65.
where the $n_i$'s are nonnegative integers whose sum is n.
The number of ways to specify a term, then,
is the number of nonnegative integer solutions to $n_1 +n_2 + ... +n_m = n$,
which by Theorem 2 is $C(m + n - 1, n)$.
Note that the coefficients C for these terms can be computed using Theorem 3—see Exercise 65.
問題7
page 457, chapter 6.5 Exercise 68
How many terms are there in the expansion of
\begin{eqnarray*}
(x + y + z)^{100} ?
\end{eqnarray*}
問題7
page 457, chapter 6.5 Exercise 68
How many terms are there in the expansion of
\begin{eqnarray*}
(x + y + z)^{100} ?
\end{eqnarray*}
By Exercise 64, the answer is
\begin{eqnarray*}
C(\underline{3} + \underline{100} - 1, \underline{100}) = C(102, \underline{100}) = \underline{5151}
\end{eqnarray*}