HW9 詳解
問題1 (a)(b)
page 608, Section 9.1 Exercise 6(a)(b)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
- $x + y = 0$
- $x = ±y$
問題1 (a)(b)
page 608, Section 9.1 Exercise 6(a)(b)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
- $x + y = 0$
- $x = ±y$
- Reflexive(反射性): A relation $R$ on a set $X$ is reflexive if $(x, x) \in R, \forall x \in X.$
- symmetric(對稱性): A relation $R$ on a set $X$ is symmetric if $\forall x,y \in X, if (x,y) \in R, then (y,x) in R.$
- antisymmetric(反對稱性): A relation $R$ on a set $X$ is antisymmetric if $\forall x,y \in X, if (x,y) \in R(A), and (y,x) \in R(B)$, then A = B.
- transitive(遞移性): A relation $R$ on a set $X$ is transitive if $\forall x,y,z \in X, if (x,y) \in R , (y,z) \in R, then (x,z) \in R.$
- Since $1+1 \not = 0$, this relation is not reflexive. Since $x+y=y+x$, it follows that $x+y=0$ if and only if $y+x=0$, so the relation is symmetric. Since $(1,-1)$ and $(-1,1)$ are both in $R$, the relation is not antisymmetric. The relation is not transitive; for example, $(1,-1) ∈ R$ and $(-1,1) ∈ R$, but $(1,1)$ $\not ∈ R$.
- Since $x = ±x$ (choosing the plug sign), the relation is reflexive. Since $x = ±y$ if and only if $y = ±x$, the relation is symmetric. Since $(1,-1)$ and $(-1,1)$ are both in $R$, the relation is not antisymmetric. The relation is transitive, essentially because the product of 1's and -1's is $±1$.
問題1 (c)(d)
page 608, Section 9.1 Exercise 6(c)(d)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
c) $x − y$ is a rational number
-
d) $x = 2y$
問題1 (c)(d)
page 608, Section 9.1 Exercise 6(c)(d)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
c) $x − y$ is a rational number
-
d) $x = 2y$
- Reflexive(反射性): A relation $R$ on a set $X$ is reflexive if $(x, x) \in R, \forall x \in X.$
- symmetric(對稱性): A relation $R$ on a set $X$ is symmetric if $\forall x,y \in X, if (x,y) \in R, then (y,x) in R.$
- antisymmetric(反對稱性): A relation $R$ on a set $X$ is antisymmetric if $\forall x,y \in X, if (x,y) \in R(A), and (y,x) \in R(B)$, then A = B.
- transitive(遞移性): A relation $R$ on a set $X$ is transitive if $\forall x,y,z \in X, if (x,y) \in R , (y,z) \in R, then (x,z) \in R.$
- c) The relation is reflexive, since $x-x=0$ is a rational number. The relation is symmetric, because if $x-y$ is rational, then so is $-(x-y) = y-x$. Since $(1,-1)$ and $(-1,1)$ are both in $R$, the relation is not antisymmetric. To see that the relation is transitive, note that if $(x,y) ∈ R$ and $(y,z) ∈ R$, then $x-y$ and $y-z$ are rational numbers. Therefore their sum $x-z$ is rational, and that means that $(x,z) ∈ R$.
- d) Since $1 \not = 2.1$,this relation is not reflexive. It is not symmetric, since $(2,1) ∈ R$, but $(1,2) \not ∈ R$. To see that it is antisymmetric, suppose that $x = 2y$ and $y = 2x$. Then $y = 4y$, from which it follows that $y = 0$ and hence $x = 0$. Thus the only time that $(x,y)$ and $(y,z)$ are both is $R$ is when $x = y$ (and both are 0). This relation is clearly not transitive, since $(4,2) ∈ R$ and $(2,1) ∈ R$, but $(4,1) \not ∈ R$.
問題1 (e)(f)
page 608, Section 9.1 Exercise 6(e)(f)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
e) $xy ≥ 0$
-
f) $xy = 0$
問題1 (e)(f)
page 608, Section 9.1 Exercise 6(e)(f)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
e) $xy ≥ 0$
-
f) $xy = 0$
- Reflexive(反射性): A relation $R$ on a set $X$ is reflexive if $(x, x) \in R, \forall x \in X.$
- symmetric(對稱性): A relation $R$ on a set $X$ is symmetric if $\forall x,y \in X, if (x,y) \in R, then (y,x) in R.$
- antisymmetric(反對稱性): A relation $R$ on a set $X$ is antisymmetric if $\forall x,y \in X, if (x,y) \in R(A), and (y,x) \in R(B)$, then A = B.
- transitive(遞移性): A relation $R$ on a set $X$ is transitive if $\forall x,y,z \in X, if (x,y) \in R , (y,z) \in R, then (x,z) \in R.$
- e) This relation is reflexive since squares are always nonnegative. It is clearly symmetric (the roles of x and y in the statement are interchangeable.) It is not antisymmetric, since $(2,3)$ and $(3,2)$ are both in $R$. It is not transitive; for example, $(1,0) ∈ R$ and $(0,-2) ∈ R$, but $(1,-2) \not ∈ R$.
- f) This is not reflexive, since $(1,1) \not ∈ R$. It is clearly symmetric (the roles of x and y in the statement are interchangeable.) It is not antisymmetric, since $(2,0)$ and $(0,2)$ are both in $R$. It is not transitive; for example, $(1,0) ∈ R$ and $(0,-2) ∈ R$, but $(1,-2) \not ∈ R$.
問題1 (g)(h)
page 608, Section 9.1 Exercise 6(g)(h)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
g) $x = 1$
-
h) $x = 1$ or $y = 1$
問題1 (g)(h)
page 608, Section 9.1 Exercise 6(g)(h)
Determine whether the relation $R$ on the set of all real
numbers is reflexive, symmetric, antisymmetric,
and/or transitive, where $(x, y) ∈ R$ if and only if
and/or transitive, where $(x, y) ∈ R$ if and only if
-
g) $x = 1$
-
h) $x = 1$ or $y = 1$
- Reflexive(反射性): A relation $R$ on a set $X$ is reflexive if $(x, x) \in R, \forall x \in X.$
- symmetric(對稱性): A relation $R$ on a set $X$ is symmetric if $\forall x,y \in X, if (x,y) \in R, then (y,x) in R.$
- antisymmetric(反對稱性): A relation $R$ on a set $X$ is antisymmetric if $\forall x,y \in X, if (x,y) \in R(A), and (y,x) \in R(B)$, then A = B.
- transitive(遞移性): A relation $R$ on a set $X$ is transitive if $\forall x,y,z \in X, if (x,y) \in R , (y,z) \in R, then (x,z) \in R.$
- g) This is not reflexive, since $(2,2) \not ∈ R$. It is not symmetric, since $(1,2) ∈ R$ but $(2,1) \not ∈ R$. It is antisymmetric, because if $(x,y) ∈ R$ and $(y,x) ∈ R$, then $x = 1$ and $y = 1$, so $x = y$. It is transitive, because if $(x,y) ∈ R$ and $(y,z) ∈ R$, then $x = 1$ (and $y = 1$, although that doesn't matter), so $(x,z) ∈ R$.
- h) This is not reflexive, since $(2,2) \not ∈ R$. It is clearly symmetric (the roles of x and y in the statement are interchangeable.) It is not antisymmetric, since $(2,1)$ and $(1,2)$ are both in $R$. It is not transitive; for example, $(3,1) ∈ R$ and $(1,7) ∈ R$, but $(3,7) \not ∈ R$.
問題2
page 619, Section 9.2 Exercise 2
Which 4-tuples are in the relation {$(a, b, c, d) ∣ a, b, c$,
and $d$ are positive integers with $abcd = 6$}?
問題2
page 619, Section 9.2 Exercise 2
Which 4-tuples are in the relation
{$(a, b, c, d) ∣ a, b, c$, and $d$ are positive integers with
$abcd = 6$}?
列舉所有abcd=6的排列
- We have to find all the solutions to this equation,making sure to include all the permutations. The 4 tuples are
-
$ \begin{align*} (6,1,1,1),(1,6,1,1),(1,1,6,1),(1,1,1,6),\\
(3,2,1,1),(3,1,2,1),(3,1,1,2),(2,3,1,1),\\
(2,1,3,1),(2,1,1,3),(1,3,2,1),(1,3,1,2),\\
(1,2,3,1),(1,2,1,3),(1,1,3,2),(1,1,2,3).\\
\end{align*} $
問題3(a)(b)
page 627, Section 9.3 Exercise 14(a)(b)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
a) $R_1\cup{R_2}$
-
b) $R_1\cap{R_2}$
問題3(a)(b)
page 627, Section 9.3 Exercise 14(a)(b)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
a) $R_1\cup{R_2}$
-
b) $R_1\cap{R_2}$
- $ \cup $ 指的是對矩陣元素做element-wise聯集
- $ \cap $ 指的是對矩陣元素做element-wise交集
-
a. The matrix for the union is formed by taking the join :
$\begin{bmatrix} 0&1&0\\1&1&1\\1&1&1 \end{bmatrix}\quad$
-
b. The matrix for the intersection is formed by taking the
meet :
$\begin{bmatrix} 0&1&0\\0&1&1\\1&0&0 \end{bmatrix}\quad$
問題3(c)(d)
page 627, Section 9.3 Exercise 14(c)(d)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
c) $R_2\circ{R_1}$
-
d) $R_1\circ{R_1}$
問題3(c)(d)
page 627, Section 9.3 Exercise 14(c)(d)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
c) $R_2\circ{R_1}$
-
d) $R_1\circ{R_1}$
- Boolean Product of Two matrix:
- $\begin{bmatrix} c11&c12&c13\\c21&c22&c23\\c31&c32&c33 \end{bmatrix}\quad$ $\begin{bmatrix} a11&a12&a13\\a21&a22&a23\\a31&a32&a33 \end{bmatrix}\quad$ $\begin{bmatrix} b11&b12&b13\\b21&b22&b23\\b31&b32&b33 \end{bmatrix}\quad$
- $ c11 = a11 \cap b11 \cup a12 \cap b21 \cup a13 \cap b31$
- 基本上類似矩陣乘法,但boolean product會是element-wise的交集然後再聯集
-
c. The matrix is the Boolean product
$M_{R_1}\odot{M_{R_2}}$:
$\begin{bmatrix} 0&1&1\\1&1&1\\0&1&0 \end{bmatrix}\quad$
-
b. The matrix is the Boolean product
$M_{R_1}\odot{M_{R_1}}$:
$\begin{bmatrix} 1&1&1\\1&1&1\\0&1&0 \end{bmatrix}\quad$
問題3(e)
page 627, Section 9.3 Exercise 14(e)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
e) $R_1\oplus{R_2}$
問題3(e)
page 627, Section 9.3 Exercise 14(e)
Let $R_1$ and $R_2$ be relations on a set A represented by the
matrices
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
$ M_{R_1}= \begin{bmatrix} 0&1&0\\1&1&1\\1&0&0 \end{bmatrix}\quad $ and $ M_{R_2}= \begin{bmatrix} 0&1&0\\0&1&1\\1&1&1 \end{bmatrix}\quad $
Find the matrices that represent
-
e) $R_1\oplus{R_2}$
- $XOR$運算符指的是相同處為0,相異處為1。
- 兩個矩陣做$XOR$,指的是矩陣元素element-wise做$XOR$。
e. The matrix is the entrywise $XOR$ :
$\begin{bmatrix} 0&0&0\\1&0&0\\0&1&1 \end{bmatrix}\quad$
$\begin{bmatrix} 0&0&0\\1&0&0\\0&1&1 \end{bmatrix}\quad$
問題4
page 638, Section 9.4 Exercise 20
Let $R$ be the relation that contains the pair $(a, b)$ if $a$
and $b$ are cities such that there is a direct nonstop airline
flight from $a$ to $b$. When is $(a, b)$ in
-
a) $R^2$?
-
b) $R^3$?
-
c) $R^*$?
問題4
page 638, Section 9.4 Exercise 20
Let $R$ be the relation that contains the pair $(a, b)$
if $a$ and $b$ are cities such that there is a direct nonstop
airline flight from $a$ to $b$.
When is $(a, b)$ in
-
a) $R^2$?
-
b) $R^3$?
-
c) $R^*$?
- a. The pair $(a,b)$ in $R^2$ precisely when there is a city $c$ such that there is a dierct flight from $a$ to $c$ and a dierct flight from $c$ to $b$ -- in other words, when it is possible to fly from $a$ to $b$ with a scheduled stop (and possibly a plane change) in some intermidiate city.
- b. The pair $(a,b)$ in $R^3$ precisely when there is a city $c$ and $d$ such that there is a dierct flight from $a$ to $c$, a dierct flight from $c$ to $d$ and a dierct flight from $d$ to $b$ -- in other words, when it is possible to fly from $a$ to $b$ with two scheduled stops (and possibly a plane change at one or both) in some intermidiate city.
- c. The pair $(a,b)$ in $R^*$ precisely when it is possible to fly from $a$ to $b$.
問題5
page 647, Section 9.5 Exercise 24
Determine whether the relations represented by these zero–one
matrices are equivalence relations.
$a) \begin{bmatrix} 1&1&1\\0&1&1\\1&1&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&1&0\\0&1&0&1\\1&0&1&0\\0&1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&1&1&0\\1&1&1&0\\1&1&1&0\\0&0&0&1 \end{bmatrix}\quad $
$a) \begin{bmatrix} 1&1&1\\0&1&1\\1&1&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&1&0\\0&1&0&1\\1&0&1&0\\0&1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&1&1&0\\1&1&1&0\\1&1&1&0\\0&0&0&1 \end{bmatrix}\quad $
問題5
page 647, Section 9.5 Exercise 24
Determine whether the relations represented by these zero–one
matrices are
equivalence relations.
$a) \begin{bmatrix} 1&1&1\\0&1&1\\1&1&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&1&0\\0&1&0&1\\1&0&1&0\\0&1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&1&1&0\\1&1&1&0\\1&1&1&0\\0&0&0&1 \end{bmatrix}\quad $
$a) \begin{bmatrix} 1&1&1\\0&1&1\\1&1&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&1&0\\0&1&0&1\\1&0&1&0\\0&1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&1&1&0\\1&1&1&0\\1&1&1&0\\0&0&0&1 \end{bmatrix}\quad $
- Equivalence Relations: A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
-
If R is a reflexive relation, all the elements on the main
diagonal of $M_R$ are equal to 1.
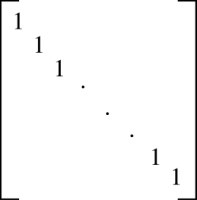
-
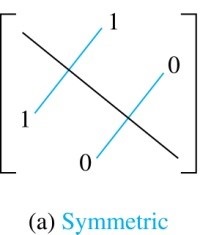
R is a symmetric relation,
if and only if $m_{ij}$ = 1 whenever $m_{ji}$ = 1.
- a) This is not an equivalence relation, since it is not symmetric.
- b) This is an equivalence relation; one equivalence class consists of the first and third elements, and the other consists of the second and fourth elements.
- c) This is an equivalence relation; one equivalence class consists of the first, second and third elements, and the other consists of the fourth elements.
問題6
page 662, Section 9.6 Exercise 8
Determine whether the relations represented by these zero–one
matrices are partial orders.
$a) \begin{bmatrix} 1&0&1\\1&1&0\\0&0&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&0\\0&1&0\\1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1 \end{bmatrix}\quad $
$a) \begin{bmatrix} 1&0&1\\1&1&0\\0&0&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&0\\0&1&0\\1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1 \end{bmatrix}\quad $
問題6
page 662, Section 9.6 Exercise 8
Determine whether the relations represented by these zero–one
matrices are
partial orders.
$a) \begin{bmatrix} 1&0&1\\1&1&0\\0&0&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&0\\0&1&0\\1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1 \end{bmatrix}\quad $
$a) \begin{bmatrix} 1&0&1\\1&1&0\\0&0&1 \end{bmatrix}\quad $ $b) \begin{bmatrix} 1&0&0\\0&1&0\\1&0&1 \end{bmatrix}\quad $ $c) \begin{bmatrix} 1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1 \end{bmatrix}\quad $
- A relation R on a set S is called a partial ordering, or partial order, if it is reflexive, antisymmetric, and transitive.
-
If R is a reflexive relation, all the elements on the main
diagonal of $M_R$ are equal to 1.

-
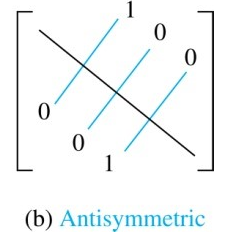
R is an antisymmetric relation,
if and only if $m_{ij}$ = 0 or $m_{ji}$ = 0 when i≠
j.
- a) This relation is $(1,1),(1,3),(2,1),(2,2),(3,3)$. It is clearly reflexive and antisymmetric. The only one pairs that might present problems with transitivity are the nondiagonal pairs, $(2,1)$ and $(1,3)$. If the relation were to be transitive, then we would also need the pair $(2,3)$ in the relation. Since it is not there, the relation is not a partial order.
- b) Reasoning as in part (a), we see that this relation is a partial order, since the pair $(3,1)$ can cause no problem with transitivity.
- c) A little trial and error shows that this relation is not transitive ($(1,3)$ and $(3,4)$ are present, but not $(1,4)$) and Therefore not a partial order.